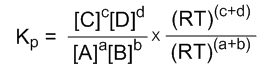KP方程式

KP方程式 (英: Kadomtsev–Petviashvili equation) は非線形波動・水面波を記述する偏微分方程式であり、次のように表わされる。

${\displaystyle \displaystyle \partial _{x}(\partial _{t}u u\partial _{x}u \epsilon ^{2}\partial _{xxx}u) \lambda \partial _{yy}u=0,\quad \lambda =\pm 1.}$

KdV方程式の2次元版方程式であり、KdV方程式と並ぶ可積分系・ソリトン方程式の代表例である。

変種

• Gardner-KP 方程式
• KP-Boussinesq 方程式
• Lax-KP 方程式
• 超離散KP方程式 (英: Ultradiscrete KP equation)

KP方程式に関連した業績のある研究者

海外

• セルゲイ・ノヴィコフ (数学者)
• en:Mark J. Ablowitz

日本

• 薩摩順吉
• 佐藤幹夫 (数学者)-佐藤理論
• 神保道夫 (三輪哲二、柏原正樹などとの共同研究)
• 広田良吾
• 和達三樹

関連項目

• 流体力学
• 可積分系
• ソリトン
• ラックス・ペア
• 広田の方法
• KdV方程式

出典

参考文献

• Kadomtsev, B. B.; Petviashvili, V. I. (1970). “On the stability of solitary waves in weakly dispersive media”. Sov. Phys. Dokl. 15: 539–541. Bibcode: 1970SPhD...15..539K. . Translation of “Об устойчивости уединенных волн в слабо диспергирующих средах”. Doklady Akademii Nauk SSSR 192: 753–756. 
• Previato, Emma (2001), “KP-equation”, in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=KP-equation 
• Kodama, Y. (2017). KP Solitons and the Grassmannians: combinatorics and geometry of two-dimensional wave patterns. Springer.
• 時弘哲治、箱玉系の数理、朝倉書店。

関連文献

和文

• 塩田隆比呂「KP方程式とSchottky問題」『数学』第41巻第1号、日本数学会、1989年、16-33頁、CRID 1390282680042479744、doi:10.11429/sugaku1947.41.16、ISSN 0039470X。 
• 藤井信太郎, 京藤敏達, 西村仁嗣「KP方程式を用いたマッハ反射の数値解析」『海岸工学論文集』第43巻、土木学会、1996年、31-35頁、CRID 1390282679526394496、doi:10.2208/proce1989.43.31、ISSN 0916-7897。 
• 応用力学研究所研究集会報告 No.16ME-S1「非線形波動の物理と数理構造」 (PDF) Reports of RIAM Symposium No.16ME-S1, Physics and Mathematical Structures of Nonlinear Waves, Proceedings of a symposium held at Chikushi Campus, Kyushu University, Kasuga, Fukuoka, Japan, November 15 - 17, 2004. Article No. 32: KP方程式による孤立波相互作用とRogue Waveの関連について, 辻英一，及川正行, A. V. Porubov.
• 塩崎峻介, 村上洋一「KP方程式における線ソリトンの不安定性に関する直接数値計算 (非線形波動現象の数理と応用)」『数理解析研究所講究録』第1645巻、京都大学数理解析研究所、157-167頁、CRID 1050282677155323392、hdl:2433/140667、ISSN 1880-2818。 
• 及川正行「第8章 KP方程式のソリトン解 : 連載—非線形波動 －ソリトンを中心として－」（PDF）『ながれ』第32巻第3号、日本流体力学会、2013年6月、251-266頁、ISSN 02863154。 

英文

• Lou, S. Y., & Hu, X. B. (1997). Infinitely many Lax pairs and symmetry constraints of the KP equation. Journal of Mathematical Physics, 38(12), 6401-6427.
• Nakamura, A. (1989). A bilinear N-soliton formula for the KP equation. Journal of the Physical Society of Japan, 58(2), 412-422.
• Kodama, Y. (2004). Young diagrams and N-soliton solutions of the KP equation. Journal of Physics A: Mathematical and General, 37(46), 11169.
• Xiao, T., & Zeng, Y. (2004). Generalized Darboux transformations for the KP equation with self-consistent sources. Journal of Physics A: Mathematical and General, 37(28), 7143.
• Minzoni, A. A., & Smyth, N. F. (1996). Evolution of lump solutions for the KP equation. Wave Motion, 24(3), 291-305.

外部リンク

• Weisstein, Eric W. "Kadomtsev–Petviashvili equation". mathworld.wolfram.com (英語).
• Gioni Biondini and Dmitri Pelinovsky (ed.). "Kadomtsev–Petviashvili equation". Scholarpedia.
• www.amath.washington.edu/~bernard/kp.html (The KP page by Bernard Deconinck, University of Washington, Department of Applied Mathematics)